Citar (formato IEEE):
Microlab IoT, «Entendiendo el Análisis Espectral: FFT, FS, DTFS, FT, DTFT, DFT,» microlab.ec. https://microlab.ec/blog/entendiendo-el-analisis-espectral (accessed: May. 3, 2022).
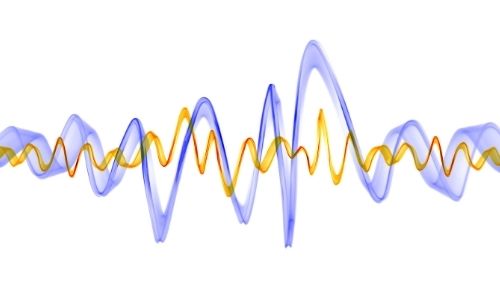
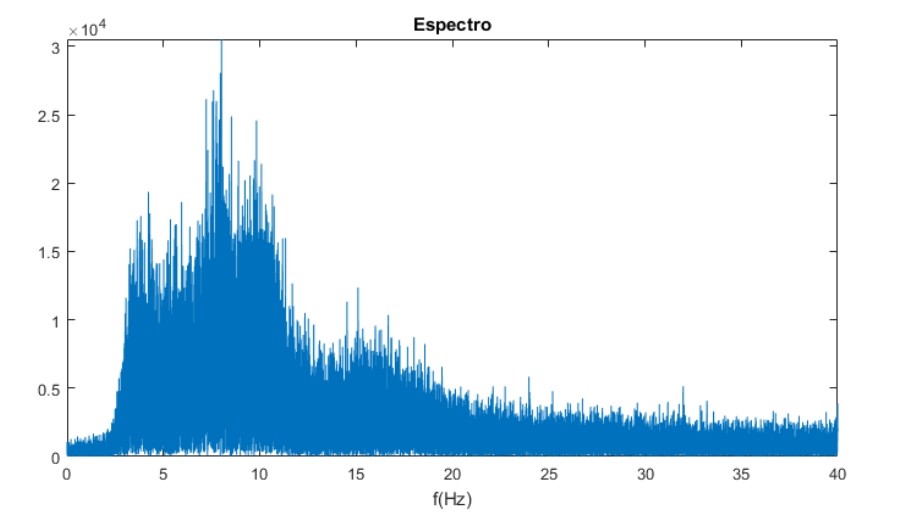
El análisis espectral es un análisis basado en la descomposición de señales en componentes sinusoidales, cada componente oscilando a una frecuencia determinada y con una amplitud determinada, es decir, se muestra se consigue una visión de la información en el dominio de la frecuencia, mostrando la contribución de cada componente de frecuencia de una señal. Esta conversión al dominio de la frecuencia se logra mediante la transformada de Fourier. El resultado del análisis de Fourier es un espectro de amplitud, con las mismas unidades de amplitud que tenía la señal en el tiempo. Un ejemplo de este análisis se muestra en la Figura 1, donde se presenta el espectro de una señal EEG (Electrocardiograma).
Transformada de Fourier
Según el tipo de señal en el dominio del tiempo (infinita/finita, discreta/continua, Periódica/No periódica) o del tipo de señal que se quiera obtener en el dominio de la frecuencia (continua/discreta) se debe aplicar el tipo de transformada adecuada.
Los nombres de las transformadas que se presentan en la Tabla 1 y en la Tabla 2 son los más aceptados y utilizados, pero pueden variar ya que éstos han evolucionado desordenadamente a lo largo de los últimos dos siglos [12].
Para señales infinitas en el tiempo, señales que se extienden al infinito negativo y positivo, al igual que sus componentes sinusoidales, existen ciertas maneras de encontrar su dual en el dominio de la frecuencia presentadas en la Tabla 1. El hecho de que las señales sean continuas en el dominio del tiempo o en el dominio de la frecuencia (número infinito de componentes de frecuencia) hace que no sea posible utilizar algoritmos computacionales para calcular las transformadas.
| Dominio | Series de Fourier (FS) | Series de Fourier en tiempo discreto (DTFS) | Transformada de Fourier para tiempo continuo (FT) | Transformada de Fourier en tiempo discreto (DTFT) |
| Tiempo | Continua Periódica | Discreta Periódica | Continua No periódica | Discreta No periódica |
| Frecuencia | Discreta No periódica | Discreta Periódica | Continua No periódica | Continua Periódica |
Los casos anteriores, por ser el espacio de tiempo infinito, no se aplica a señales reales y son analizados para señales teóricas. Para casos reales, con un espacio de tiempo finito se tienen los métodos presentados en la tabla 2.
| Espacio de tiempo finito | Transformada Discreta de Fourier (DFT) | Transformada Rápida de Fourier (FFT) |
| Descripción | Muestreo en frecuencia de la DTFT | Algoritmo para resolver la DTF |
| Tiempo | Discreta No periódica | Discreta No periódica |
| Frecuencia | Discreta Periódica | Discreta Periódica |
Estimación de la densidad espectral de potencia
Denominado periodograma, cuyo objetivo es determinar el contenido de cada componente de frecuencia en una señal. El proceso para la determinación del periodograma es el que se muestra en la Figura 2, donde la herramienta fundamental es la Transformada Discreta de Fourier (DTF) la cual puede ser calculada utilizando el algoritmo de la Transformada Rápida de Fourier (FFT).
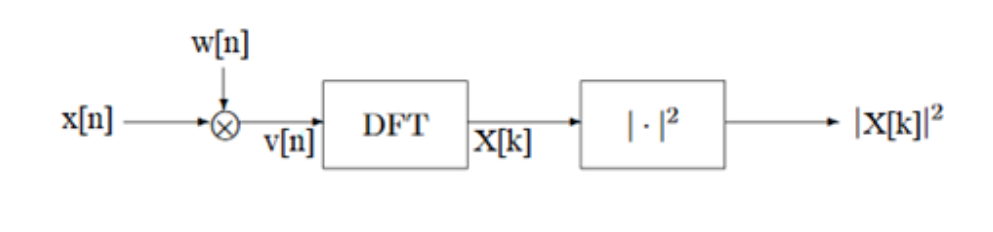
Debido a que para obtener segmentos de la señal se utiliza una ventana rectangular, es decir se multiplica la señal original por una señal rectangular para obtener un segmento del tamaño de la ventana, se produce una disminución de la resolución en frecuencia lo que produce también fuga espectral. La mayor resolución en frecuencia que se podría obtener es el ancho del espectro de la ventana rectangular.
La DTF se puede calcular como se muestra en Ecuación 1.
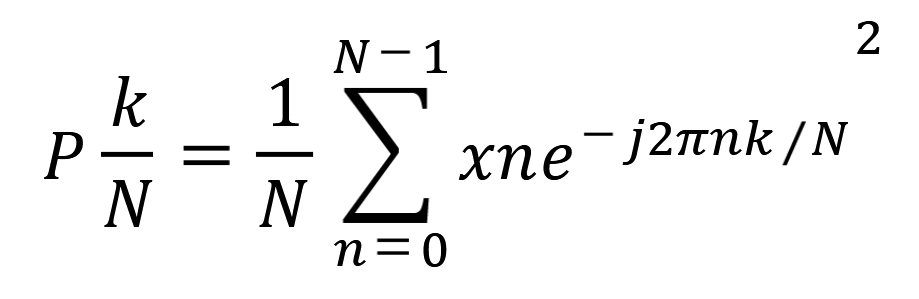
Donde: kN, frecuencias ; k=0, 1, 2, … , N-1; N, es el número de muestras de la señal en el dominio del tiempo.
Sin embargo, si se tiene una señal discreta en el dominio del tiempo de N muestras, por defecto se tendría una señal en el dominio de la frecuencia de N muestras, sin embargo, si N es demasiado pequeña la señal en el dominio de la frecuencia no podrá ser bien representada ya que tendrá muy pocas muestras. Debido a esto se recure a realizar un relleno de ceros a la señal en el dominio del tiempo aumentando su tamaño de N a L, con lo también se aumenta la densidad de puntos para representar la señal resultante en frecuencia, este cambio se muestra en la Ecuación 2.
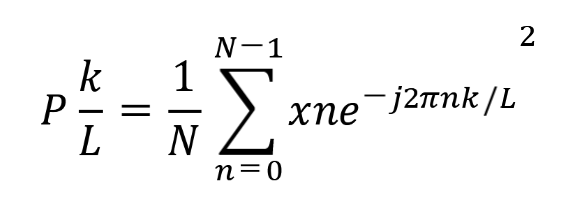
El resultado es una gráfica parecida a la obtenida en el cálculo del espectro donde se utilizó únicamente la transformada de Fourier como se muestra en la Figura 3.
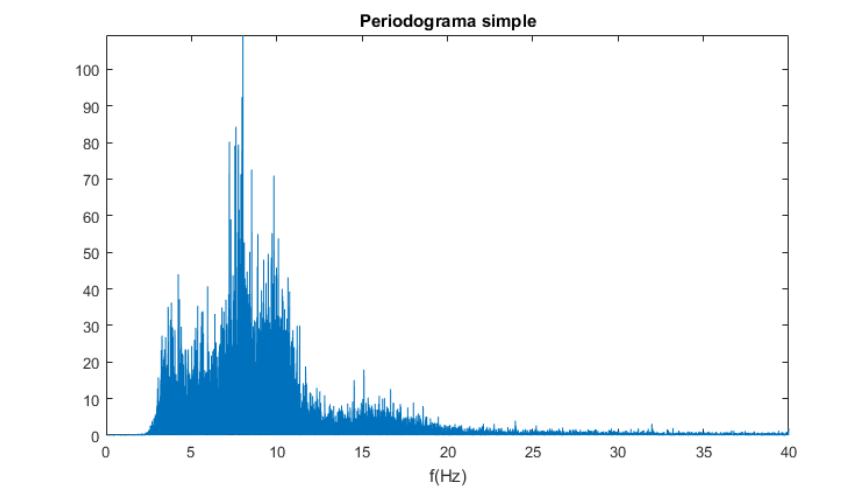
Periodograma simple, utiliza una ventana del tipo rectangular, mientras si se utiliza otro tipo de ventanas se denomina periodograma modificado, el uso de diferentes tipos de ventanas provee una mejor resolución en frecuencia, es decir, menor fuga espectral.
Método Welch para la estimación espectral de potencia
Además del periodograma y el periodograma modificado existen métodos que buscan disminuir la varianza en la estimación de la densidad espectral de potencia, es decir, generar una curva más suave, a costa de disminuir la resolución en frecuencia. Uno de estos métodos es el Método Welch. En la Figura 4 se muestran algunos de los métodos más conocidos para la estimación de la densidad espectral de potencia.
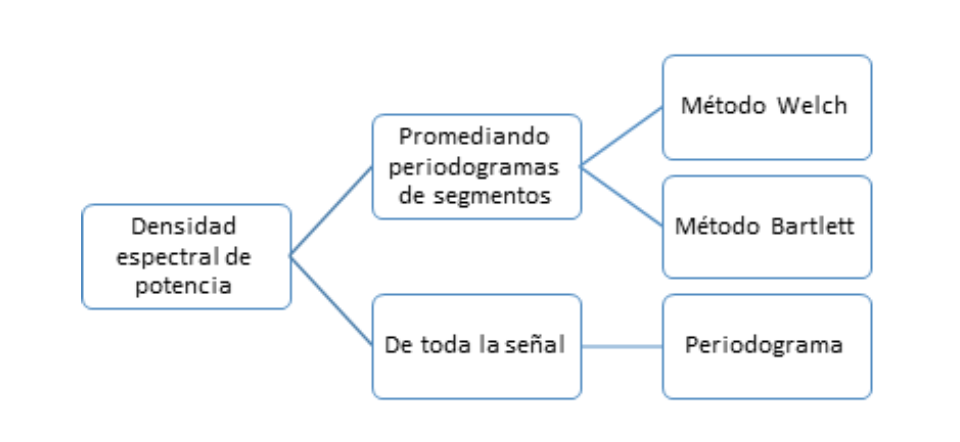
El método Welch para la estimación del espectro de potencia se basa en tres pasos fundamentales:
Primero, divide la señal original en segmentos que pueden estar o no solapados, como en la Ecuación 3.
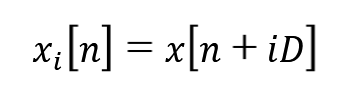
Donde: i=0, 1, …, L-1; n=0, 1, …, M-1; D, es el número de inicio de la secuencia i; N, el número de muestras de la señal en el tiempo; M, longitud del segmento; L, número de segmentos.
Por ejemplo, si se tiene una señal en el dominio del tiempo x[n] con 10 muestras (N=10) y se requiere un sobrelapamiento del 50% de muestras (D=M/2=2), un tamaño del segmento de 4 muestras (M=4), entonces se tendrían las siguientes series:
- Para i=0: x0=x0, x1, x3,x[4]
- Para i=0: x0=x2, x3, x4,x[5]
- Para i=0: x0=x4, x5, x6,x[7]
- Para i=0: x0=x6, x7, x8,x[9]
Segundo, se calcula el periodograma modificado de cada segmento como en la Ecuación 4.
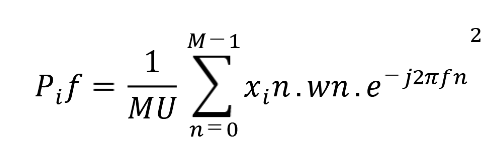
Donde: x=0, 1, …, L-1; U es un factor de normalización.
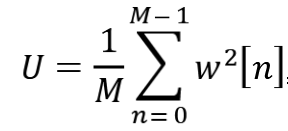
Tercero, promedia los periodogramas de todos los L segmentos como en la Ecuación 5.
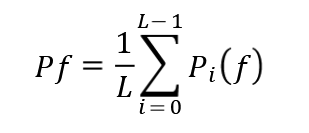
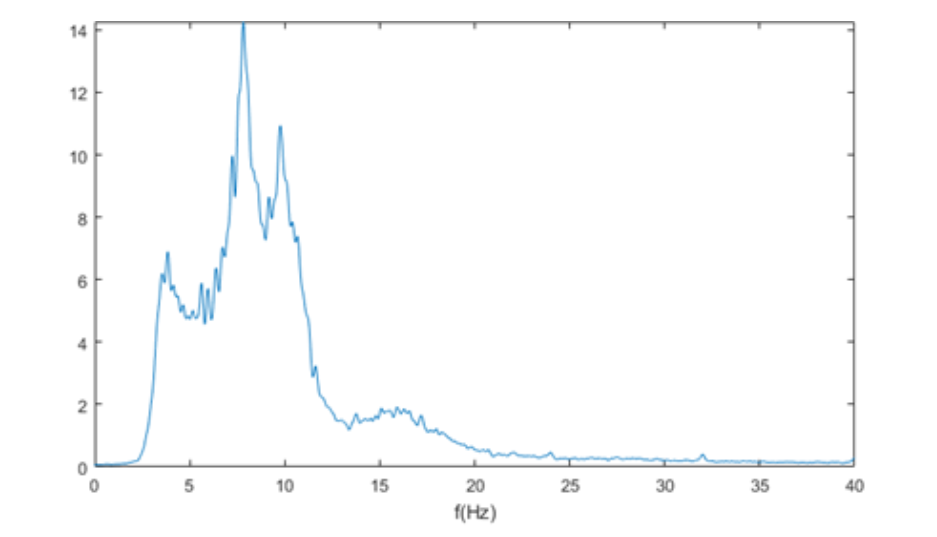
El promediado de los periodogramas hace que la curva de la densidad espectral de potencia sea más suave a diferencia de la gráfica que se consigue utilizando el periodograma simple. La Figura 5 muestra la densidad espectral de la misma señal que se utilizó para calcular el periodograma de la Figura 3.
Bibliografía:
- [1] S. W. Smith, Digital signal processing, pp. 180, Second Edition. San Diego – California: California Technical Publiching, 1999. https://users.dimi.uniud.it/~antonio.dangelo/MMS/materials/Guide_to_Digital_Signal_Process.pdf [2] https://en.wikipedia.org/wiki/Discrete-time_Fourier_transform
- [2] https://en.wikipedia.org/wiki/Discrete-time_Fourier_transform
Al buscar señales en una serie diaria de Temperatura máxima, en la frecuencia cero, se encuentra la amplitud máxima. En las demás frecuencias la amplitud es cero. ¿Cómo interpretar ese resultado? Al menos debería observarse la señal estacional.
El hecho de que la amplitud máxima se encuentre en la frecuencia cero indica que la señal tiene un componente constante o de tendencia a lo largo del tiempo. En otras palabras, la temperatura máxima tiene una cierta tendencia a aumentar o disminuir a lo largo del tiempo, pero no presenta cambios periódicos.
En cuanto a la señal estacional, su componente podría no aparecer en el espectro por no representar un peso significativo en la señal o porque la serie temporal está abarcando un solo periodo por lo que no se registra la periodicidad del evento.
Es importante analizar la señal de manera completa y en su contexto para poder interpretar adecuadamente los resultados.